Introduction
Step 1 is the first tutorial that will walk you through how to compute an outplace Fourier Transform in parallel. The goal is not just to compute FFTs, but to introduce different functions of the library, and explain some of the concepts. In this step you will get familiar with AccFFT routines and learn a few things about computing distributed, parallel FFTs.
The goal is to compute forward FFT of an array of size which is distributed in parallel to processes.
That is each process will get pencils of size . This is shown below schematically:
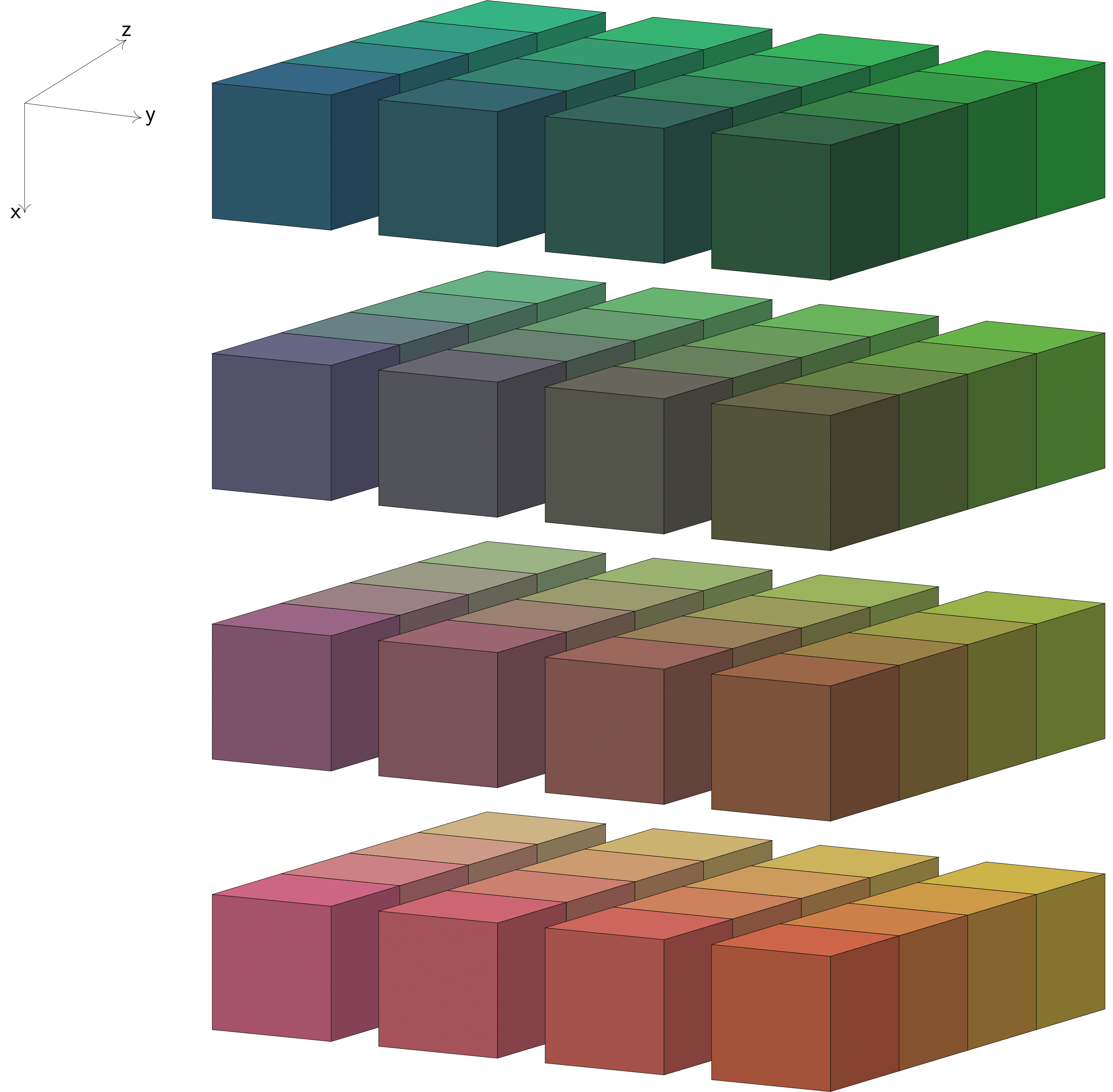
To compute a 3D distributed FFT, AccFFT first computes a batched FFT along the last dimension and then performs a global transpose so that each process gets the second dimension locally. A similar operation is performed again to get the first dimension locally. For this reason the output of forward transform would be distributed as follows:
Note that the memory access layout is the same for both input and output. The only difference is that the input array is distributed along the first and second dimension, while the output array is distributed along the second and third. Some of the libraries do change the memory layout as well, but AccFFT does not do that. This makes it very easy for the user to use the same functions for both the input and output arrays, without any changes.
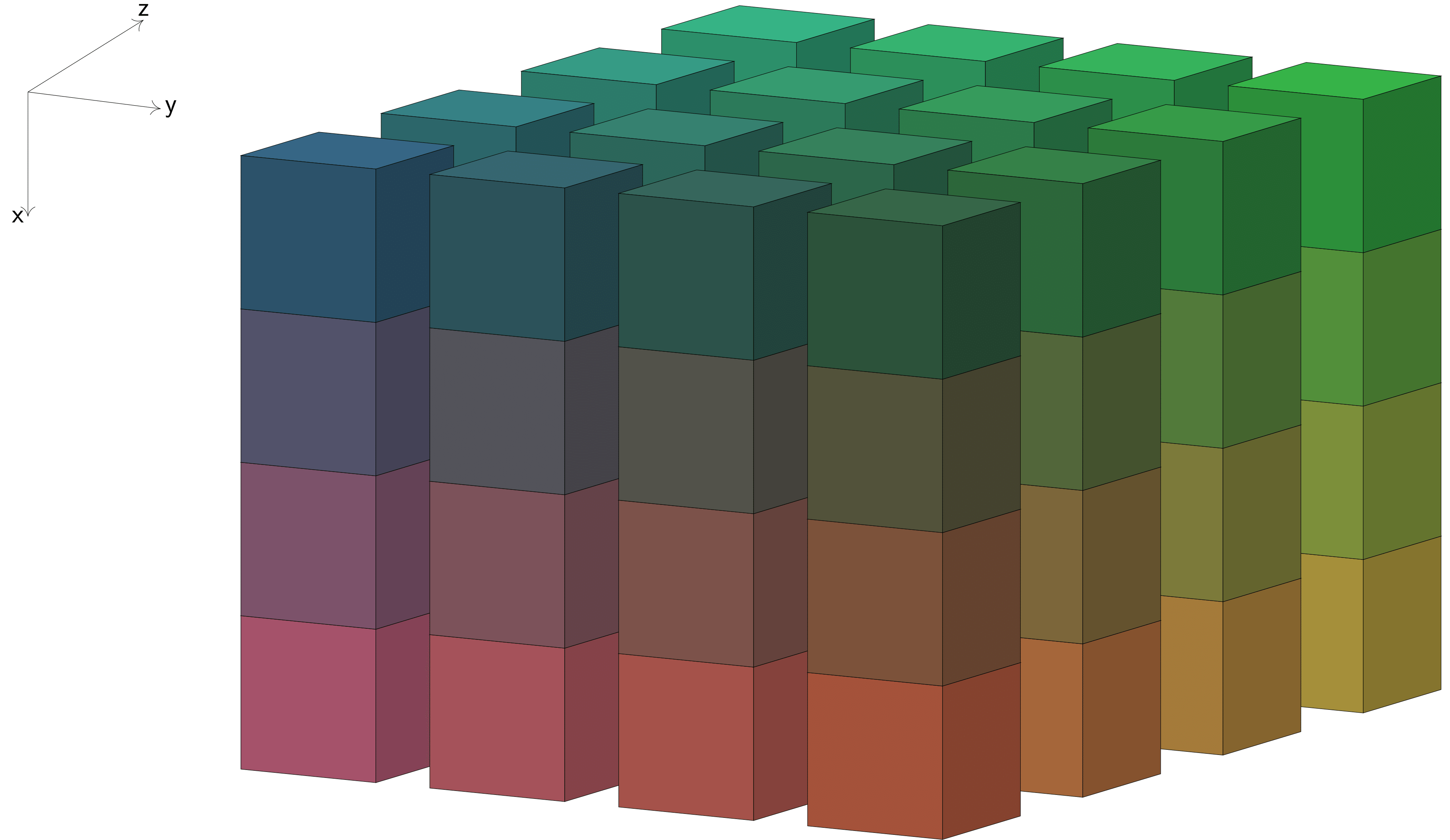
It is very important that you understand how the data is distributed among processes. If the above is not clear for you, please read the AccFFT paper.
Code Explanation
So first of all, we need to include mpi and accfft header files. The makefile inside step1 folder will provide the location for the “< accfft.h >”, if the library is installed correctly.
Then we have the following function declarations: initialize function initializes the double array data, with the formula provided by testcase function. As you can see, the latter gets the X, Y, Z coordinates and returns the value of a Gaussian centered at . That will be the test function that will be used here. There is also a check_err function, which will compute the error in our computations and the main part of the code which is the step1 function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <mpi.h>
#include <accfft.h>
void initialize(double *data,int*n, MPI_Comm c_comm);
inline double testcase(double X,double Y,double Z){
double sigma= 4;
double pi=4*atan(1.0);
double analytic;
analytic= (std::exp( -sigma * ( (X-pi)*(X-pi) + (Y-pi)*(Y-pi) +(Z-pi)*(Z-pi) )));
if(analytic!=analytic) analytic=0; /* Do you think the condition will be false always? */
return analytic;
}
void check_err(double* data,int*n,MPI_Comm c_comm);
void step1(int *n, int nthreads);
NaN! Why do you think the if condition at line 11 is needed?
Now let’s take a look at step1 function. First, we get the number of processes and the id of each process among all participating mpi ranks. Then we create a 2d Cartesian grid, named c_comm, using these mpi ranks. The grid sizes of c_comm can be controlled with c_dims. If you do specify a correct grid size with c_dims, the accfft_create_comm function will use those values. Otherwise, it will print an error message and corrects your c_dims and creates c_comm. Now, by correct I mean that the following condition should be met:
This is rather obvious, but most of the time people forget to set it correctly. As you can see, here we do not set it to any value, and we let the library itself to choose them. Next is the declaration for the data and data_hat arrays. data will store the input function, and the FFT of data will be written to data_hat array. The rest of the declarations are for measuring some timing statistics.
1
2
3
4
5
6
7
8
9
10
11
12
void step1(int *n, int nthreads) {
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD,&nprocs);
/* Create Cartesian Communicator */
int c_dims[2];
MPI_Comm c_comm;
accfft_create_comm(MPI_COMM_WORLD,c_dims,&c_comm);
double *data,*data_hat;
double f_time=0*MPI_Wtime(),i_time=0, setup_time=0;
Now note that we have an input array that is distributed among a 2d grid of processes. We need to know which block corresponds to each process. This can be found by calling accfft_local_size_dft_r2c function. The inputs to the function is the array size, n, and the 2d grid communicator, c_comm. With this info, it gives you isize, istart, osize, and ostart of the processor calling it. The i refers to input and o refers to output. So isize is the size of the block belonging to the MPI process (the size of the pencil in Figure 1). Similarly, osize is the output size that this process gets after the FFT is performed (the size of the pencil in Figure 2). The istart and ostart arrays provide you with the exact starting location of the block that this process owns. So for example, consider a 256x256x256 input with 4 processors that are decomposed into a 2x2 grid. Process zero will get a block of size 128x128x256 for the isize. The istart for process zero will be (0,0,0), and for process one, it will be (0,64,0).
Now the story is the same for the osize, but with a small little difference. For real-to-complex transforms, the output is a little larger than the input. This is because of the Nyquist frequency. This means that a real-to-complex FFT of a array will be complex numbers. So for an array of size 256x256x256, the FFT will be an array of 256x256x130 complex numbers. Now, according to Figure 2 this array is distributed in the second and third dimensions. So for the above 4 processor example, process zero will get osize of (256,128,65) complex numbers.
To make your life easier, the accfft_local_size_dft_r2c computes how much allocation is required for the output array. You can also compute the allocation size of the input array using isize.
Always use this approach to allocate the output array as the required size may not be the same as the input array. Moreover, for strange processor grid cases the allocation size might be larger than what you get from the osize array. So be safe, fasten your seat belt and use the alloc_max!
1
2
3
4
5
6
7
/* Get the local pencil size and the allocation size */
int alloc_max=0;
int isize[3],osize[3],istart[3],ostart[3];
alloc_max=accfft_local_size_dft_r2c(n,isize,istart,osize,ostart,c_comm);
data=(double*)accfft_alloc(isize[0]*isize[1]*isize[2]*sizeof(double)));
data_hat=(double*)accfft_alloc(alloc_max);
Next we initialize the library with accfft_init function. The function gets an integer to set the number of OpenMP threads. In general, for small array sizes you will not get a noticeable speedup with OpenMP. So just set it to one is ok. However, for very large transform sizes, you may benefit from it. Next we setup a plan using accfft_plan_dft_3d_r2c_c2r funciton. This function will setup different FFT plans, global transpose functions, etc. As you can see, the function gets a flag as its last argument. The flag is used to test different routines to optimize performance. You can use the following options:
- ACCFFT_ESTIMATE
- ACCFFT_MEASURE
- ACCFFT_PATIENT
Note that the third option will considerably increase the setup time. The default option is ACCFFT_MEASURE
To simplify everyone’s life (and save memory) you do not need to create a separate plan for complex-to-real transform. The only exception is the rare case where you have to apply the FFT plan to an array with a different allocation layout. This would never be the case if you use accfft_alloc functions. But if you have to do it, then you can simply create two plans using the same function
After all of this we call the initialize function, which sets the input array to a Gaussian centered at .
1
2
3
4
5
6
7
8
9
accfft_init(nthreads);
setup_time=-MPI_Wtime();
/* Create FFT plan */
accfft_plan * plan=accfft_plan_dft_3d_r2c_c2r(n,data,(double*)data_hat,c_comm,ACCFFT_MEASURE);
setup_time+=MPI_Wtime();
/* Initialize data */
initialize(data,n,c_comm);
MPI_Barrier(c_comm);
Next we perform the FFT transform! This is simply done by calling accfft_execute_r2c function. As you know, if we perform and IFFT transform on the output, we should get the original array with a scaling. So let’s do that and check whether we get the original array or not. We can perform the IFFT transform using the accfft_execute_c2r function. We write the output to data2 array.
1
2
3
4
5
6
7
8
9
10
11
12
/* Perform forward FFT */
f_time-=MPI_Wtime();
accfft_execute_r2c(plan,data,data_hat);
f_time+=MPI_Wtime();
MPI_Barrier(c_comm);
/* Perform backward FFT */
i_time-=MPI_Wtime();
accfft_execute_c2r(plan,data_hat,data2);
i_time+=MPI_Wtime();
Now the difference between data and data2 array must be zero if everything is computed correctly. However, as mentioned in the previous article, there will be a scaling required for data2.
1
2
3
4
5
6
7
8
9
10
11
/* Check Error */
double err=0,g_err=0;
double norm=0,g_norm=0;
for (int i=0;i<isize[0]*isize[1]*isize[2];++i){
err+=data2[i]/n[0]/n[1]/n[2]-data[i];
norm+=data2[i]/n[0]/n[1]/n[2];
}
MPI_Reduce(&err,&g_err,1, MPI_DOUBLE, MPI_MAX,0, MPI_COMM_WORLD);
MPI_Reduce(&norm,&g_norm,1, MPI_DOUBLE, MPI_SUM,0, MPI_COMM_WORLD);
PCOUT<<"\n Error is "<<g_err<<std::endl;
As you can see, we need to compute the global difference between the two arrays, so an MPI reduction is performed to compute the max error. You could have also checked the error using check_err(data2,n,c_comm) command. It calls the test function to get the analytical form of the solution and compares it to data2. The rest of the code is straight forward. We perform similar reductions to compute the maximum time that each section took and print them to stdout.
PCOUT is the same as std::cout, with the difference that only the root process will write the output.
GPU Code
The GPU version of the code can be found in step1_gpu.cpp file. The implementation is very similar to the CPU, except that most of the function names need to be appended by _gpu. For example, note that the code in using accfft_gpu.h instead of accfft.h. Or that the FFT plan type is accfft_plan_gpu instad of accfft_plan. That’s it on the user side! Everything else is taken care in the background!
The step1_gpu code first allocates and initializes data on the cpu, and writes it into data_cpu. Then this data is transferred to a GPU buffer called data. The data transfer is not necessary, and you can simply use a cuda kernel to initialize the GPU array (look at initialize_gpu function in kernels.cu). After this step, the forward and backward FFT operations are performed on GPU. Finally, the result is transferred back to the CPU to check the error (Obviously this can be done on the GPU as well.)
Note that the design of the library allows you to use both the CPU and GPU functionalities simultaneously. For example, you can run some FFTs on CPU and some other FFTs on GPU. You only need to include both accfft.h and accfft_gpu.h, and use the corresponding functions.
Results
You can make and run the code as follows:
make
ibrun/mpirun -np 4 step1 512 512 512Whether you need to use ibrun to mpirun to spawn mpi processes depends on your system. The np option sets the number of processes to 4 and the last three inputs set the size of the array. The executable prints the following when run on one node of Maverick:
ERROR c_dims!=nprocs --> 0*0 !=4
Switching to c_dims_0=2 , c_dims_1=2
Switching to c_dims_0=2 , c_dims_1=2
Error is 5.28468e-12
Relative Error is 1.88332e-09
Timing for FFT of size 512*512*512
Setup 18.9544
FFT 0.86937
IFFT 0.861248The ERROR is because we did not set c_dims and the library corrects it for us and sets it to 2x2. Running the same configuration on one K40 GPU of Maverick gives the following result:
make
ibrun/mpirun -np 4 step1_gpu 512 512 512ERROR c_dims!=nprocs --> 0*0 !=4
Switching to c_dims_0=2 , c_dims_1=2
Error is 1.69119e-11
Relative Error is 4.49042e-17
Results are CORRECT!
GPU Timing for FFT of size 512*512*512
Setup 1.08223
FFT 0.565722
IFFT 0.570743Note that here I am using only one GPU, but still the problem is divided into four smaller ones. You can try running it on four seperate GPUs on different nodes and compare the timings. I also suggest testing different problem sizes, and comparing CPU and GPU times. In general, the GPU will be faster for large problem sizes.
Complete CPU Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
/*
* File: step1.cpp
* License: Please see LICENSE file.
* AccFFT: Massively Parallel FFT Library
* Created by Amir Gholami on 12/23/2014
* Email: contact@accfft.org
*/
#include <stdlib.h>
#include <math.h> // M_PI
#include <mpi.h>
#include <accfft.h>
void initialize(double *a, int*n, MPI_Comm c_comm);
inline double testcase(double X, double Y, double Z) {
double sigma = 4;
double pi = M_PI;
double analytic;
analytic = std::exp(-sigma * ((X - pi) * (X - pi) + (Y - pi) * (Y - pi)
+ (Z - pi) * (Z - pi)));
if (analytic != analytic)
analytic = 0; /* Do you think the condition will be false always? */
return analytic;
} // end testcase
void check_err(double* a, int*n, MPI_Comm c_comm);
void step1(int *n, int nthreads);
void step1(int *n, int nthreads) {
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Create Cartesian Communicator */
int c_dims[2] = { 0 };
MPI_Comm c_comm;
accfft_create_comm(MPI_COMM_WORLD, c_dims, &c_comm);
double *data;
Complex *data_hat;
double f_time = 0 * MPI_Wtime(), i_time = 0, setup_time = 0;
int alloc_max = 0;
int isize[3], osize[3], istart[3], ostart[3];
/* Get the local pencil size and the allocation size */
alloc_max = accfft_local_size_dft_r2c(n, isize, istart, osize, ostart,
c_comm);
//data=(double*)accfft_alloc(isize[0]*isize[1]*isize[2]*sizeof(double));
data = (double*) accfft_alloc(alloc_max);
data_hat = (Complex*) accfft_alloc(alloc_max);
accfft_init(nthreads);
/* Create FFT plan */
setup_time = -MPI_Wtime();
accfft_plan * plan = accfft_plan_dft_3d_r2c(n, data, (double*) data_hat,
c_comm, ACCFFT_MEASURE);
setup_time += MPI_Wtime();
/* Warm Up */
accfft_execute_r2c(plan, data, data_hat);
accfft_execute_r2c(plan, data, data_hat);
/* Initialize data */
initialize(data, n, c_comm);
MPI_Barrier(c_comm);
/* Perform forward FFT */
f_time -= MPI_Wtime();
accfft_execute_r2c(plan, data, data_hat);
f_time += MPI_Wtime();
MPI_Barrier(c_comm);
double * data2 = (double*) accfft_alloc(
isize[0] * isize[1] * isize[2] * sizeof(double));
/* Perform backward FFT */
i_time -= MPI_Wtime();
accfft_execute_c2r(plan, data_hat, data2);
i_time += MPI_Wtime();
/* Check Error */
double err = 0, g_err = 0;
double norm = 0, g_norm = 0;
for (int i = 0; i < isize[0] * isize[1] * isize[2]; ++i) {
err += std::abs(data2[i] / n[0] / n[1] / n[2] - data[i]);
norm += std::abs(data[i]);
}
MPI_Reduce(&err, &g_err, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&norm, &g_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
PCOUT << "\nError is " << g_err << std::endl;
PCOUT << "Relative Error is " << g_err / g_norm << std::endl;
if (g_err / g_norm < 1e-10)
PCOUT << "\nResults are CORRECT!\n\n";
else
PCOUT << "\nResults are NOT CORRECT!\n\n";
/* Compute some timings statistics */
double g_f_time, g_i_time, g_setup_time;
MPI_Reduce(&f_time, &g_f_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&i_time, &g_i_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&setup_time, &g_setup_time, 1, MPI_DOUBLE, MPI_MAX, 0,
MPI_COMM_WORLD);
PCOUT << "Timing for FFT of size " << n[0] << "*" << n[1] << "*" << n[2]
<< std::endl;
PCOUT << "Setup \t" << g_setup_time << std::endl;
PCOUT << "FFT \t" << g_f_time << std::endl;
PCOUT << "IFFT \t" << g_i_time << std::endl;
accfft_free(data);
MPI_Barrier(c_comm);
accfft_free(data_hat);
accfft_free(data2);
accfft_destroy_plan(plan);
accfft_cleanup();
MPI_Comm_free(&c_comm);
return;
} // end step1
int main(int argc, char **argv) {
int NX, NY, NZ;
MPI_Init(&argc, &argv);
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Parsing Inputs */
if (argc == 1) {
NX = 128;
NY = 128;
NZ = 128;
} else {
NX = atoi(argv[1]);
NY = atoi(argv[2]);
NZ = atoi(argv[3]);
}
int N[3] = { NX, NY, NZ };
int nthreads = 1;
step1(N, nthreads);
MPI_Finalize();
return 0;
} // end main
void initialize(double *a, int *n, MPI_Comm c_comm) {
double pi = M_PI;
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c(n, isize, istart, osize, ostart, c_comm);
#pragma omp parallel
{
double X, Y, Z;
long int ptr;
#pragma omp for
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n[2] + j * n[2] + k;
a[ptr] = testcase(X, Y, Z);
}
}
}
}
return;
} // end initialize
void check_err(double* a, int*n, MPI_Comm c_comm) {
int nprocs, procid;
MPI_Comm_rank(c_comm, &procid);
MPI_Comm_size(c_comm, &nprocs);
long long int size = n[0];
size *= n[1];
size *= n[2];
double pi = 4 * atan(1.0);
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c(n, isize, istart, osize, ostart, c_comm);
double err = 0, norm = 0;
double X, Y, Z, numerical_r;
long int ptr;
int thid = omp_get_thread_num();
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n[2] + j * n[2] + k;
numerical_r = a[ptr] / size;
if (numerical_r != numerical_r)
numerical_r = 0;
err += std::abs(numerical_r - testcase(X, Y, Z));
norm += std::abs(testcase(X, Y, Z));
}
}
}
double g_err = 0, g_norm = 0;
MPI_Reduce(&err, &g_err, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Reduce(&norm, &g_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
PCOUT << "\nL1 Error of iFF(a)-a: " << g_err << std::endl;
PCOUT << "Relative L1 Error of iFF(a)-a: " << g_err / g_norm << std::endl;
if (g_err / g_norm < 1e-10)
PCOUT << "\nResults are CORRECT!\n\n";
else
PCOUT << "\nResults are NOT CORRECT!\n\n";
return;
} // end check_err
Complete GPU Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
/*
* License: Please see LICENSE file.
* AccFFT: Massively Parallel FFT Library
* Email: contact@accfft.org
*/
/*
* File: step1_gpu.cpp
* Contributed by Pierre Kestener
*/
#include <stdlib.h>
#include <math.h> // M_PI
#include <mpi.h>
#include <cuda_runtime_api.h>
#include <accfft_gpu.h>
void initialize(double *a, int*n, MPI_Comm c_comm);
void initialize_gpu(double *a, int*n, int* isize, int * istart);
void check_err(double* a, int*n, MPI_Comm c_comm);
void step1_gpu(int *n) {
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Create Cartesian Communicator */
int c_dims[2] = { 0 };
MPI_Comm c_comm;
accfft_create_comm(MPI_COMM_WORLD, c_dims, &c_comm);
double *data, *data_cpu;
Complex *data_hat;
double f_time = 0 * MPI_Wtime(), i_time = 0, setup_time = 0;
int alloc_max = 0;
int isize[3], osize[3], istart[3], ostart[3];
/* Get the local pencil size and the allocation size */
alloc_max = accfft_local_size_dft_r2c_gpu(n, isize, istart, osize, ostart,
c_comm);
data_cpu = (double*) malloc(
isize[0] * isize[1] * isize[2] * sizeof(double));
//data_hat=(Complex*)accfft_alloc(alloc_max);
cudaMalloc((void**) &data, isize[0] * isize[1] * isize[2] * sizeof(double));
cudaMalloc((void**) &data_hat, alloc_max);
//accfft_init(nthreads);
/* Create FFT plan */
setup_time = -MPI_Wtime();
accfft_plan_gpu * plan = accfft_plan_dft_3d_r2c_gpu(n, data,
(double*) data_hat, c_comm, ACCFFT_MEASURE);
setup_time += MPI_Wtime();
/* Warm Up */
accfft_execute_r2c_gpu(plan, data, data_hat);
accfft_execute_r2c_gpu(plan, data, data_hat);
/* Initialize data */
initialize(data_cpu, n, c_comm);
cudaMemcpy(data, data_cpu, isize[0] * isize[1] * isize[2] * sizeof(double),
cudaMemcpyHostToDevice);
// initialize_gpu(data,n,isize,istart); // GPU version of initialize function
MPI_Barrier(c_comm);
/* Perform forward FFT */
f_time -= MPI_Wtime();
accfft_execute_r2c_gpu(plan, data, data_hat);
f_time += MPI_Wtime();
MPI_Barrier(c_comm);
double *data2_cpu, *data2;
cudaMalloc((void**) &data2,
isize[0] * isize[1] * isize[2] * sizeof(double));
data2_cpu = (double*) malloc(
isize[0] * isize[1] * isize[2] * sizeof(double));
/* Perform backward FFT */
i_time -= MPI_Wtime();
accfft_execute_c2r_gpu(plan, data_hat, data2);
i_time += MPI_Wtime();
/* copy back results on CPU */
cudaMemcpy(data2_cpu, data2,
isize[0] * isize[1] * isize[2] * sizeof(double),
cudaMemcpyDeviceToHost);
/* Check Error */
double err = 0, g_err = 0;
double norm = 0, g_norm = 0;
for (int i = 0; i < isize[0] * isize[1] * isize[2]; ++i) {
err += std::abs(data2_cpu[i] / n[0] / n[1] / n[2] - data_cpu[i]);
norm += std::abs(data_cpu[i]);
}
MPI_Reduce(&err, &g_err, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Reduce(&norm, &g_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
PCOUT << "\nL1 Error is " << g_err << std::endl;
PCOUT << "Relative L1 Error is " << g_err / g_norm << std::endl;
if (g_err / g_norm < 1e-10)
PCOUT << "\nResults are CORRECT!\n\n";
else
PCOUT << "\nResults are NOT CORRECT!\n\n";
check_err(data2_cpu, n, c_comm);
/* Compute some timings statistics */
double g_f_time, g_i_time, g_setup_time;
MPI_Reduce(&f_time, &g_f_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&i_time, &g_i_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&setup_time, &g_setup_time, 1, MPI_DOUBLE, MPI_MAX, 0,
MPI_COMM_WORLD);
PCOUT << "GPU Timing for FFT of size " << n[0] << "*" << n[1] << "*" << n[2]
<< std::endl;
PCOUT << "Setup \t" << g_setup_time << std::endl;
PCOUT << "FFT \t" << g_f_time << std::endl;
PCOUT << "IFFT \t" << g_i_time << std::endl;
free(data_cpu);
free(data2_cpu);
cudaFree(data);
cudaFree(data_hat);
cudaFree(data2);
accfft_destroy_plan_gpu(plan);
accfft_cleanup_gpu();
MPI_Comm_free(&c_comm);
return;
} // end step1_gpu
inline double testcase(double X, double Y, double Z) {
double sigma = 4;
double pi = M_PI;
double analytic;
analytic = std::exp(-sigma * ((X - pi) * (X - pi) + (Y - pi) * (Y - pi)
+ (Z - pi) * (Z - pi)));
if (analytic != analytic)
analytic = 0; /* Do you think the condition will be false always? */
return analytic;
}
void initialize(double *a, int *n, MPI_Comm c_comm) {
double pi = M_PI;
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c_gpu(n, isize, istart, osize, ostart, c_comm);
#pragma omp parallel
{
double X, Y, Z;
long int ptr;
#pragma omp for
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n[2] + j * n[2] + k;
a[ptr] = testcase(X, Y, Z);
}
}
}
}
return;
} // end initialize
void check_err(double* a, int*n, MPI_Comm c_comm) {
int nprocs, procid;
MPI_Comm_rank(c_comm, &procid);
MPI_Comm_size(c_comm, &nprocs);
long long int size = n[0];
size *= n[1];
size *= n[2];
double pi = 4 * atan(1.0);
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c_gpu(n, isize, istart, osize, ostart, c_comm);
double err = 0, norm = 0;
double X, Y, Z, numerical_r;
long int ptr;
int thid = omp_get_thread_num();
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n[2] + j * n[2] + k;
numerical_r = a[ptr] / size;
if (numerical_r != numerical_r)
numerical_r = 0;
err += std::abs(numerical_r - testcase(X, Y, Z));
norm += std::abs(testcase(X, Y, Z));
}
}
}
double g_err = 0, g_norm = 0;
MPI_Reduce(&err, &g_err, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Reduce(&norm, &g_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
PCOUT << "\nL1 Error of iFF(a)-a: " << g_err << std::endl;
PCOUT << "Relative L1 Error of iFF(a)-a: " << g_err / g_norm << std::endl;
if (g_err / g_norm < 1e-10)
PCOUT << "\nResults are CORRECT!\n\n";
else
PCOUT << "\nResults are NOT CORRECT!\n\n";
return;
} // end check_err
int main(int argc, char **argv) {
int NX, NY, NZ;
MPI_Init(&argc, &argv);
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Parsing Inputs */
if (argc == 1) {
NX = 128;
NY = 128;
NZ = 128;
} else {
NX = atoi(argv[1]);
NY = atoi(argv[2]);
NZ = atoi(argv[3]);
}
int N[3] = { NX, NY, NZ };
step1_gpu(N);
MPI_Finalize();
return 0;
} // end main