Introduction
Step 2 is the second tutorial that will walk you through how to compute an inplace real-to-complex (R2C) FFT. There is a subtlety here, in that the result of R2C FFT requires a larger memory than its input. As a result, the user needs to allocate additional memory for the input so that the extra data would fit in the memory. However, that is not all; the user has to use a special padded access pattern in the spatial domain. First an explanation of why there is a memory overhead:
The complex result of a R2C FFT is conjugate symmetric. What this mean is that half of the output data is equal to the conjugate of the other half. So it is really not required to compute those frequencies. This property saves half of the computations and requires half memory. The exact computational cost of computing all the frequencies of a power 2 FFT is , and using this property it would reduce to .
So where is the memory padding? The devil is in the Nyquist frequency! The output of an R2C FFT would be complex numbers. That means you need to allocate memory, which is larger than .
Note that if we had not used the conjugate symmetry property you had to allocate , which is almost twice the above.
AccFFT gives you the right amount of memory to allocate, by calling accfft_local_size_dft_r2c function. So this is already done, however the user must use a special format for initializing the data. The additional allocated memory is stored as if the input matrix was of size . The last dimension is still , but when one wants to access elements in memory this padding must be respected.
For example, to access/initialize the (i,j,k) element of the data in the spatial domain (i.e. before doing the R2C transform), one should access .
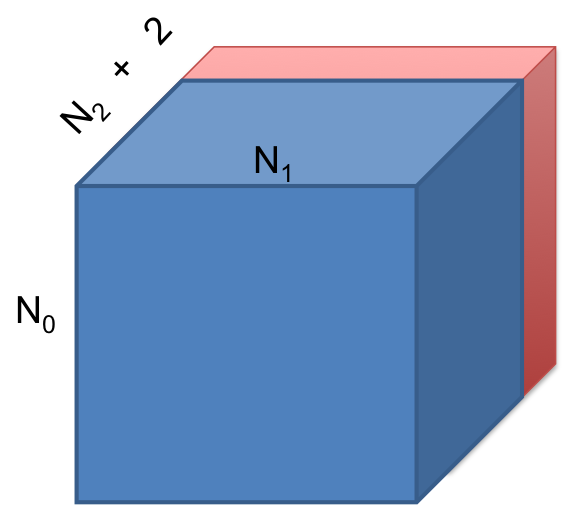
As you would see in Step 3, there is no such issue for inplace complex-to-complex transforms. That is because, there is no conjugate property for that case!
Code Explanation
The code for this step is very similar to step1, so I would just point out the important differences.
First note that the allocation size is alloc_max which is returned by calling accfft_local_size_dft_r2c function:
1
2
3
4
5
6
/* Get the local pencil size and the allocation size */
int alloc_max=0;
int isize[3],osize[3],istart[3],ostart[3];
alloc_max=accfft_local_size_dft_r2c(n,isize,istart,osize,ostart,c_comm);
data=(double*)accfft_alloc(alloc_max);
This ensures that the data on each process has enough memory to store the output of R2C transform. Moreover, note that the library would create an inplace transform if the second and third arguments of accfft_plan_dft_3d_r2c point to the same memory address (Otherwise an outplace transform would be created).
1
2
/* Create FFT plan */
accfft_plan * plan=accfft_plan_dft_3d_r2c(n,data,data,c_comm,ACCFFT_MEASURE);
Finally, note that initialize and check_err functions are a little different than step1. The padded version of is used to read/write data into the spatial array.
1
2
3
4
/* Padded access pattern */
int n2_=(n[2]/2+1)*2;
int ptr=( i*n[1]+j )*n2_+k;
a[ptr]=testcase(X,Y,Z);
Results
You can make and run the code as follows:
make
ibrun/mpirun -np 4 step2 128 128 128On my machine, I get an output like this:
ERROR c_dims!=nprocs --> 0*0 !=4
Switching to c_dims_0=2 , c_dims_1=2
L1 Error of iFF(a)-a: 1.33786e-11
Relative L1 Error of iFF(a)-a: 2.27345e-15
Results are CORRECT!
Timing for FFT of size 128*128*128
Setup 0.67326
FFT 0.00962496
IFFT 0.00752997Again, the ERROR is because we were lazy and did not set c_dims. The library corrects it for us and sets it to an appropriate value.
I suggest you run the program with different sizes and different number of MPI processes, and compare the timings with that of step 1.
GPU Code
The GPU version of the code can be found in step2_gpu.cpp file. Note that in this step, I use a GPU kernel to initialize the data instead of first initializing it on CPU and copying it over.
Complete CPU Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
/*
* File: step2.cpp
* License: Please see LICENSE file.
* AccFFT: Massively Parallel FFT Library
* Created by Amir Gholami on 12/23/2014
* Email: contact@accfft.org
*/
#include <stdlib.h>
#include <math.h>
#include <mpi.h>
#include <accfft.h>
inline double testcase(double X, double Y, double Z) {
double sigma = 4;
double pi = 4 * atan(1.0);
double analytic = 0;
analytic = (std::exp(-sigma * ((X - pi) * (X - pi) + (Y - pi) * (Y - pi)
+ (Z - pi) * (Z - pi))));
if (analytic != analytic)
analytic = 0;
return analytic;
} // end testcase
void initialize(double *a, int*n, MPI_Comm c_comm);
void check_err(double* a, int*n, MPI_Comm c_comm);
void step2(int *n, int nthreads);
void initialize(double *a, int*n, MPI_Comm c_comm) {
int nprocs, procid;
MPI_Comm_rank(c_comm, &procid);
MPI_Comm_size(c_comm, &nprocs);
double pi = M_PI;
// Note that n2_ is the padded version of n2 which is
// the spatial size of the array. To access the spatial members
// we must use n2_, because that is how it is written in memory!
int n2_ = (n[2] / 2 + 1) * 2;
// Get the local pencil size and the allocation size
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c(n, isize, istart, osize, ostart, c_comm);
#pragma omp parallel
{
double X, Y, Z;
long int ptr;
#pragma omp for
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n2_ + j * n2_ + k;
a[ptr] = testcase(X, Y, Z);
}
}
}
}
return;
} // end initialize
void check_err(double* a, int*n, MPI_Comm c_comm) {
int nprocs, procid;
MPI_Comm_rank(c_comm, &procid);
MPI_Comm_size(c_comm, &nprocs);
long long int size = n[0];
size *= n[1];
size *= n[2];
double pi = 4 * atan(1.0);
// Note that n2_ is the padded version of n2 which is
// the spatial size of the array. To access the spatial members
// we must use n2_, because that is how it is written in memory!
int n2_ = (n[2] / 2 + 1) * 2;
// Get the local pencil size and the allocation size
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c(n, isize, istart, osize, ostart, c_comm);
double err = 0, norm = 0;
{
double X, Y, Z, numerical;
long int ptr;
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n2_ + j * n2_ + k;
numerical = a[ptr] / size;
if (numerical != numerical)
numerical = 0;
err += std::abs(numerical - testcase(X, Y, Z));
norm += std::abs(testcase(X, Y, Z));
//std::cout<<"("<<i<<","<<j<<","<<k<<") "<<numerical<<'\t'<<testcase(X,Y,Z)<<std::endl;
}
}
}
}
double g_err = 0, g_norm = 0;
MPI_Reduce(&err, &g_err, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Reduce(&norm, &g_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
PCOUT << "\nL1 Error of iFF(a)-a: " << g_err << std::endl;
PCOUT << "Relative L1 Error of iFF(a)-a: " << g_err / g_norm << std::endl;
if (g_err / g_norm < 1e-10)
PCOUT << "\nResults are CORRECT!\n\n";
else
PCOUT << "\nResults are NOT CORRECT!\n\n";
return;
} // end check_err
void step2(int *n, int nthreads) {
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Create Cartesian Communicator */
int c_dims[2];
MPI_Comm c_comm;
accfft_create_comm(MPI_COMM_WORLD, c_dims, &c_comm);
double *data;
double f_time = 0 * MPI_Wtime(), i_time = 0, setup_time = 0;
int alloc_max = 0;
int isize[3], osize[3], istart[3], ostart[3];
/* Get the local pencil size and the allocation size */
alloc_max = accfft_local_size_dft_r2c(n, isize, istart, osize, ostart,
c_comm);
data = (double*) accfft_alloc(alloc_max);
accfft_init(nthreads);
setup_time = -MPI_Wtime();
/* Create FFT plan */
accfft_plan * plan = accfft_plan_dft_3d_r2c(n, data, data, c_comm,
ACCFFT_MEASURE); // note that in and out are both data -> inplace plan
setup_time += MPI_Wtime();
/* Warm Up */
accfft_execute_r2c(plan, data, (Complex*) data);
accfft_execute_r2c(plan, data, (Complex*) data);
/* Initialize data */
initialize(data, n, c_comm); // special initialize plan for inplace transform -> difference in padding
MPI_Barrier(c_comm);
/* Perform forward FFT */
f_time -= MPI_Wtime();
accfft_execute_r2c(plan, data, (Complex*) data);
f_time += MPI_Wtime();
MPI_Barrier(c_comm);
/* Perform backward FFT */
i_time -= MPI_Wtime();
accfft_execute_c2r(plan, (Complex*) data, data);
i_time += MPI_Wtime();
/* Check Error */
check_err(data, n, c_comm);
/* Compute some timings statistics */
double g_f_time, g_i_time, g_setup_time;
MPI_Reduce(&f_time, &g_f_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&i_time, &g_i_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&setup_time, &g_setup_time, 1, MPI_DOUBLE, MPI_MAX, 0,
MPI_COMM_WORLD);
PCOUT << "Timing for FFT of size " << n[0] << "*" << n[1] << "*" << n[2]
<< std::endl;
PCOUT << "Setup \t" << g_setup_time << std::endl;
PCOUT << "FFT \t" << g_f_time << std::endl;
PCOUT << "IFFT \t" << g_i_time << std::endl;
accfft_free(data);
accfft_destroy_plan(plan);
accfft_cleanup();
MPI_Comm_free(&c_comm);
return;
} // end step2
int main(int argc, char **argv) {
int NX, NY, NZ;
MPI_Init(&argc, &argv);
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Parsing Inputs */
if (argc == 1) {
NX = 128;
NY = 128;
NZ = 128;
} else {
NX = atoi(argv[1]);
NY = atoi(argv[2]);
NZ = atoi(argv[3]);
}
int N[3] = { NX, NY, NZ };
int nthreads = 1;
step2(N, nthreads);
MPI_Finalize();
return 0;
} // end main
Complete GPU Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
/*
* File: step2_gpu.cpp
* License: Please see LICENSE file.
* AccFFT: Massively Parallel FFT Library
* Created by Amir Gholami on 06/04/2015
* Email: contact@accfft.org
*/
#include <stdlib.h>
#include <math.h>
#include <mpi.h>
#include <cuda_runtime_api.h>
//#include <accfft.h>
#include <accfft_gpu.h>
void initialize_gpu(double *a, int*n, int* isize, int * istart);
void check_err(double* a, int*n, MPI_Comm c_comm);
double testcase(double X, double Y, double Z);
void step2_gpu(int *n) {
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Create Cartesian Communicator */
int c_dims[2];
MPI_Comm c_comm;
accfft_create_comm(MPI_COMM_WORLD, c_dims, &c_comm);
double *data, *data_cpu;
Complex *data_hat;
double f_time = 0 * MPI_Wtime(), i_time = 0, setup_time = 0;
int alloc_max = 0;
int isize[3], osize[3], istart[3], ostart[3];
/* Get the local pencil size and the allocation size */
alloc_max = accfft_local_size_dft_r2c_gpu(n, isize, istart, osize, ostart,
c_comm);
/* Note that both need to be allocated by alloc_max because of inplace transform*/
data_cpu = (double*) malloc(alloc_max);
cudaMalloc((void**) &data, alloc_max);
//accfft_init(nthreads);
/* Create FFT plan */
setup_time = -MPI_Wtime();
accfft_plan_gpu * plan = accfft_plan_dft_3d_r2c_gpu(n, data, data, c_comm,
ACCFFT_MEASURE);
setup_time += MPI_Wtime();
/* Warm Up */
accfft_execute_r2c_gpu(plan, data, (Complex*) data);
accfft_execute_r2c_gpu(plan, data, (Complex*) data);
/* Initialize data */
initialize_gpu(data, n, isize, istart);
MPI_Barrier(c_comm);
/* Perform forward FFT */
f_time -= MPI_Wtime();
accfft_execute_r2c_gpu(plan, data, (Complex*) data);
f_time += MPI_Wtime();
MPI_Barrier(c_comm);
/* Perform backward FFT */
i_time -= MPI_Wtime();
accfft_execute_c2r_gpu(plan, (Complex*) data, data);
i_time += MPI_Wtime();
/* copy back results on CPU */
cudaMemcpy(data_cpu, data, alloc_max, cudaMemcpyDeviceToHost);
/* Check Error */
check_err(data_cpu, n, c_comm);
/* Compute some timings statistics */
double g_f_time, g_i_time, g_setup_time;
MPI_Reduce(&f_time, &g_f_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&i_time, &g_i_time, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&setup_time, &g_setup_time, 1, MPI_DOUBLE, MPI_MAX, 0,
MPI_COMM_WORLD);
PCOUT << "GPU Timing for FFT of size " << n[0] << "*" << n[1] << "*" << n[2]
<< std::endl;
PCOUT << "Setup \t" << g_setup_time << std::endl;
PCOUT << "FFT \t" << g_f_time << std::endl;
PCOUT << "IFFT \t" << g_i_time << std::endl;
free(data_cpu);
cudaFree(data);
accfft_destroy_plan_gpu(plan);
accfft_cleanup_gpu();
MPI_Comm_free(&c_comm);
return;
} // end step2_gpu
void check_err(double* a, int*n, MPI_Comm c_comm) {
int nprocs, procid;
MPI_Comm_rank(c_comm, &procid);
MPI_Comm_size(c_comm, &nprocs);
long long int size = n[0];
size *= n[1];
size *= n[2];
double pi = 4 * atan(1.0);
// Note that n2_ is the padded version of n2 which is
// the spatial size of the array. To access the spatial members
// we must use n2_, because that is how it is written in memory!
int n2_ = (n[2] / 2 + 1) * 2;
// Get the local pencil size and the allocation size
int istart[3], isize[3], osize[3], ostart[3];
accfft_local_size_dft_r2c_gpu(n, isize, istart, osize, ostart, c_comm);
double err = 0, norm = 0;
{
double X, Y, Z, numerical;
long int ptr;
for (int i = 0; i < isize[0]; i++) {
for (int j = 0; j < isize[1]; j++) {
for (int k = 0; k < isize[2]; k++) {
X = 2 * pi / n[0] * (i + istart[0]);
Y = 2 * pi / n[1] * (j + istart[1]);
Z = 2 * pi / n[2] * k;
ptr = i * isize[1] * n2_ + j * n2_ + k;
numerical = a[ptr] / size;
if (numerical != numerical)
numerical = 0;
err += std::abs(numerical - testcase(X, Y, Z));
norm += std::abs(testcase(X, Y, Z));
//std::cout<<"("<<i<<","<<j<<","<<k<<") "<<numerical<<'\t'<<testcase(X,Y,Z)<<std::endl;
}
}
}
}
double g_err = 0, g_norm = 0;
MPI_Reduce(&err, &g_err, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Reduce(&norm, &g_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
PCOUT << "\nL1 Error of iFF(a)-a: " << g_err << std::endl;
PCOUT << "Relative L1 Error of iFF(a)-a: " << g_err / g_norm << std::endl;
if (g_err / g_norm < 1e-10)
PCOUT << "\nResults are CORRECT!\n\n";
else
PCOUT << "\nResults are NOT CORRECT!\n\n";
return;
} // end check_err
int main(int argc, char **argv) {
int NX, NY, NZ;
MPI_Init(&argc, &argv);
int nprocs, procid;
MPI_Comm_rank(MPI_COMM_WORLD, &procid);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
/* Parsing Inputs */
if (argc == 1) {
NX = 128;
NY = 128;
NZ = 128;
} else {
NX = atoi(argv[1]);
NY = atoi(argv[2]);
NZ = atoi(argv[3]);
}
int N[3] = { NX, NY, NZ };
step2_gpu(N);
MPI_Finalize();
return 0;
} // end main